Turm auf 6-eckigem Grundriß: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[Category:Werkstoffkunde]] | ||
__FORCETOC__ | __FORCETOC__ | ||
| − | |||
| − | |||
[[Bild:Kirchturm 6eck 3d.png|left]] | [[Bild:Kirchturm 6eck 3d.png|left]] | ||
| + | ==Aufgabe== | ||
Die Dachfläche des Kirchturms auf 6-eckigem Grundriß soll eingedeckt werden. Zu berechnen ist die Dachfläche. | Die Dachfläche des Kirchturms auf 6-eckigem Grundriß soll eingedeckt werden. Zu berechnen ist die Dachfläche. | ||
| Zeile 9: | Zeile 9: | ||
==Dachflächenberechnung== | ==Dachflächenberechnung== | ||
| + | Die Tiefe (Gegenkathete im grünen Dreieck) ist genauso lang wie die Ankathete in dem blauen Dreick, dass als weitere Information die Dachneigung enthält. | ||
| + | |||
| + | Damit läßt sich dann z.B. mit Hilfe der [[Anwendung der Tangens-Funktion|Winkelfunktion tan]] und dem [[Lehrsatz des Pythagoras]] die Sparrenlänge einer Fläche ermitteln. Die Gesamtdachfläche ist das sechsfache der Einzelfläche. | ||
==Gratlänge== | ==Gratlänge== | ||
| + | |||
| + | Zur Berechnung eines Grates kann man z.B. ein weiteres Dreieck in einer Dachfläche einzeichnen, bei dem der Sparren die erste Kathete, die halbe Trauflänge die zweite Kathete und der Grat die Hypotenuse ist. Dann läßt sich erneut mit Hilfe des [[Lehrsatz des Pythagoras|Lehrsatzes von Pythagoras]] eine Gratlänge ermitteln. | ||
==Links== | ==Links== | ||
* [[Dachflächenberechnung#Pyramide gleicher Dachneigung|Turm auf quadratischem Grundriß]] | * [[Dachflächenberechnung#Pyramide gleicher Dachneigung|Turm auf quadratischem Grundriß]] | ||
* [[Turm auf 8-eckigem Grundriß]] | * [[Turm auf 8-eckigem Grundriß]] | ||
Aktuelle Version vom 29. Dezember 2010, 10:09 Uhr
Aufgabe
Die Dachfläche des Kirchturms auf 6-eckigem Grundriß soll eingedeckt werden. Zu berechnen ist die Dachfläche.
Infos zum Grundriß
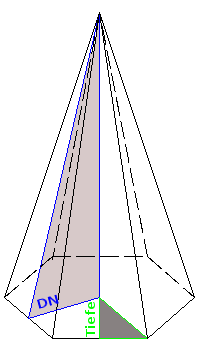
Der Grundriß ist ein 6-Eck. Wegen der Geometrie des Sechsecks muss zur Berechnung nur die Länge einer Kante angegeben sein. Daraus läßt sich denn die Tiefe (siehe grünes Dreick) und die Grundfläche berechnen.
Dachflächenberechnung
Die Tiefe (Gegenkathete im grünen Dreieck) ist genauso lang wie die Ankathete in dem blauen Dreick, dass als weitere Information die Dachneigung enthält.
Damit läßt sich dann z.B. mit Hilfe der Winkelfunktion tan und dem Lehrsatz des Pythagoras die Sparrenlänge einer Fläche ermitteln. Die Gesamtdachfläche ist das sechsfache der Einzelfläche.
Gratlänge
Zur Berechnung eines Grates kann man z.B. ein weiteres Dreieck in einer Dachfläche einzeichnen, bei dem der Sparren die erste Kathete, die halbe Trauflänge die zweite Kathete und der Grat die Hypotenuse ist. Dann läßt sich erneut mit Hilfe des Lehrsatzes von Pythagoras eine Gratlänge ermitteln.