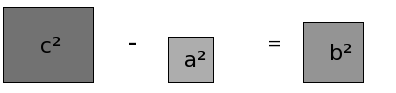Lehrsatz des Pythagoras
Einführung

|
Im rechtwinkligen Dreieck gilt der Lehrsatz des Pythagoras, der besagt
c² = a² + b² Also die Summe der beiden Quadrate über den Katheten entspricht der Größe nach dem Quadrat über der Hypotenuse. Eine Möglichkeit den Lehrsatz zu beweisen findet man hier. |
Gesucht: Hypotenuse
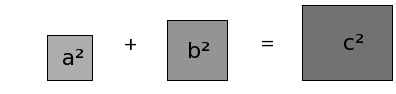
|
Sind also die Längen beider Katheten gegeben, so kann man die Größe des Quadrates über c ermitteln.
Die Länge von c ergibt sich, indem man die Wurzel aus c² zieht: |
Gesucht: Kathete
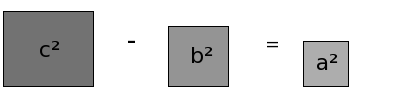
|
Sind also die Längen einer Kathete und der Hypotenuse gegeben, so kann man die Größe des Quadrates über der zweiten Kathete ermitteln.
Die Länge von a bzw b ergibt sich, indem man die Wurzel aus a² bzw b² zieht: |
Beispiele
Gesucht ist in diesem Beispiel die Hypotenuse, also ist die Gleichung
c² = a² + b²
anzuwenden. In unserem Beispiel ist das
6.28² + 7.23² = 39.44 + 52.28 = 91.72
Zieht man aus der Zahl 91.72 die Wurzel, so erhält man das Ergebnis
c = 9.58
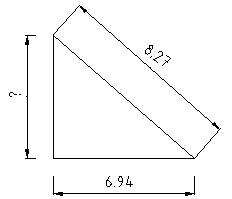
Gesucht ist in diesem Beispiel eine Kathete, also ist die Gleichung
c² - a² = b²
anzuwenden. In unserem Beispiel ist das
8.27² - 6.94² = 68.39 - 48.16 = 20.23
Zieht man aus der Zahl 20.23 die Wurzel, so erhält man das Ergebnis
b = 4.5