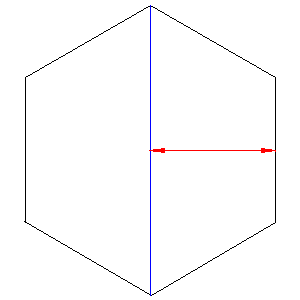
Geometrie des Sechsecks
Herleitung
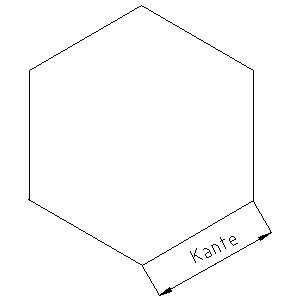
Zu berechnen ist die Fläche eines Sechsecks. Gegeben ist die Länge einer Dachkante.
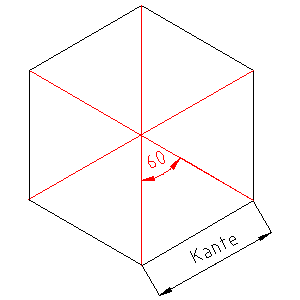
Dazu kann man die Dreiecke in das Sechseck eintragen. Da die Winkel der Dreiecke in der Mitte alle gleich groß sind, ermittelt sich der Winkel zu
360° : 6 = 60°
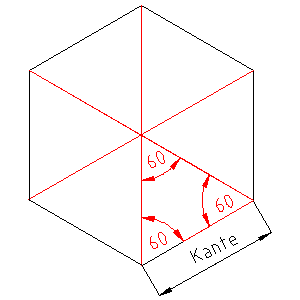
Die Summe der Innenwinkel eines Dreiecks beträgt 180°. Die beiden übrigen Winkel müssen also zusammen 120° betragen. Da sie gleich groß sind, betragen auch sie jeweils
120° : 2 = 60°.
Sind aber alle Winkel eines Dreickes gleich, so müssen auch alle Seiten des Dreiecks gleich lang sein. In der Folge heißt das für ein Sechseck:
In einem Sechseck sind alle Seiten gleich lang.
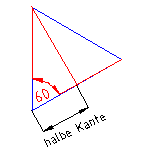
Betrachtet man dieses Dreieck näher und errichtet die Senkrechte auf einer Seite, so kann man die Länge dieser Mittelsenkrechten (MS) mit Hilfe der Winkelfunktion tan ermitteln aus
MS = (halbe Kantenlänge) * tan 60°
Somit hat man alle Informationen zur Bestimmung der Fläche des Sechsecks. Dabei gibt es zwei Möglichkeiten.
Entweder man ermittelt die Fläche eines Dreiecks und multipliziert das Ergebnis mit 6 ...
... oder man errechnet die Fläche zweier Trapeze wie nebenstehend abgebildet. Da wie oben beschrieben alle Linien im Sechseck gleich lang sind, beträgt die Länge der blauen Linie zweimal der Länge der Kante. Die Fläche eines Trapezes ist also:
Die Fläche ist das Doppelte dieses Ergebnisse.
Beispiel
Kantenlänge: 6.20 m
Also ist die Länge der Mittelsenkrechte
3.10 m * tan 60 = 5.37 m
Also ist die Fläche eines Trapezes
3* 6.20 m * 5.37 m/2 = 49.94 m²
Gesamtfläche ist also 99.88 m²