Steigung in Prozent
Einführung
Neigungen kann man in Grad oder in Prozent angeben. Dabei werden flachere Dachneigungen in Prozent und höhere in Grad angegeben.
|
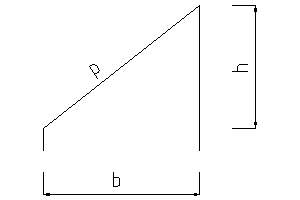
Bei der Steigungsberechnung in Prozent hat man vereinbart, dass die Breite eines rechtwinkligen (!) Dreiecks der mathematische Grundwert und die Höhe der Prozentwert der Breite ist. |
Es gilt die Gleichung ![]() zur Ermittlung der Höhe.
zur Ermittlung der Höhe.
Durch Formelumstellung kann man die Gleichungen zur Ermittlung von Breite oder des Prozentsatzes erhalten.
Eine weitere Möglichkeit besteht darin, den Zusammenhang als Dreisatz aufzustellen und mit dem Verfahren des geraden Dreisatzes zu lösen. Denn je größer der Prozentsatz, desto größer ist der Höhenunterschied und umgekehrt.
Aufgabenstellungen
Bestimme die Höhe
geg.: Breite und Prozent Steigung
ges.: Höhe
Lösung: Gesucht ist der Prozentwert, der sich mathematisch berechnet aus P = (G*p)/100. Wie oben beschrieben ist aber der Grundwert b, p die Prozentsteigung und die Höhe h der Prozentwert. Also gilt
denn, wenn man die Aufgabe als geraden Dreisatz aufstellt, gilt
| % | m | |
| 100% | <=> | Breite b |
| p% | <=> | xxx |
also, oben rechts anfangend und entgegen dem Uhrzeigersinn vorgehend teilt man jetzt zunächst die Zahlen und multipliziert anschließend. Also
![]()
Bestimme das Breitenmaß
geg.: Höhe und Prozent Steigung
ges.: Breite
Lösung: Gesucht ist der Grundwert, der sich mathematisch berechnet aus G = (P* 100)/p. Wie oben beschrieben ist aber der Grundwert b, p die Prozentsteigung und die Höhe h der Prozentwert. Also gilt
denn, wenn man die Aufgabe als geraden Dreisatz aufstellt, gilt
| % | m | |
| p% | <=> | Höhe h |
| 100% | <=> | xxx |
also, oben rechts anfangend und entgegen dem Uhrzeigersinn vorgehend teilt man jetzt zunächst die Zahlen und multipliziert anschließend. Also
![]()
Bestimme die Steigung in Prozent
geg.: Breite und Höhe
ges.: Prozentsteigung
Lösung: Gesucht ist der Prozentsatz, der sich mathematisch berechnet aus p = (P* 100)/G. Wie oben beschrieben ist aber der Grundwert b, p die Prozentsteigung und die Höhe h der Prozentwert. Also gilt
Denn, wenn man die Aufgabe als geraden Dreisatz aufstellt, gilt
| m | % | |
| Breite b | <=> | 100% |
| Höhe h | <=> | xxx |
so dass, oben rechts anfangend und entgegen dem Uhrzeigersinn vorgehend, wie in den beiden vorangehenden Fällen, man erhält:
![]()