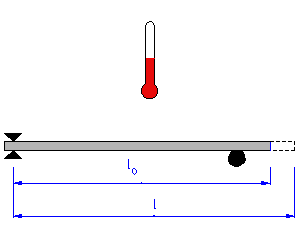
Thermische Längenänderung von Metallen

Beschreibung

Feste Körper ändern bei Erwärmung oder Abkühlung ihr Volumen und ihre Form. Im Baubereich treten vor allem Längenänderungen auf, durch die in Bauteilen Spannungen entstehen, die häufig zu Schäden führen. Der Dachdecker muss die temperaturbedingten Längenänderungen von Bauteilen berechnen können, um durch bauliche Maßnahmen Schäden zu vermeiden.
Von Längenänderungen sind in erster Linie Metalle betroffen, nicht nur weil sie sich mehr ausdehnen als andere Baustoffe, sondern auch, weil sie in größeren Längen eingebaut werden. Eine Schare (Metallband) wird bei Erwärmung länger; kühlt sie ab, zieht sie sich wieder zusammen.
Der Verbundwerkstoff Stahlbeton funktioniert u. a. aufgrund der Tatsache, dass Stahl und Beton annähernd die gleiche Dehnungszahl haben.

Berechnung

Die Längenänderung eines Bauteils wird nach folgender Formel ermittelt:

Δl = α * l0 * ΔT

so dass die Länge l dann

l = l0 + α * l0 * ΔT

beträgt.

Dabei bedeuten:

• Δl (sprich: Delta l) Längenänderung in mm

• α (sprich: Alpha) gibt an, um wieviel mm sich ein Baustoff von 1 m Länge bei einem Temperaturunterschied von 1 Kelvin ausdehnt oder zusammenzieht.
• l Einbaulänge des Bauteils in m
• Δt (sprich: Delta t) Temperaturdifferenz in Kelvin (K)

Wichtige Temperaturdehnungszahlen von Baustoffen

Baustoff	Temperaturdehnungszahl α in mm je m Länge und Grad Temperaturdifferenz
Ziegel-Mauerwerk	0,006
Beton	0,0118
Baustahl	0,012
Kupfer	0,017
Titan Zink	0,022
Aluminium	0,024
Blei	0,02
PVC	0,08

Beispielberechnung

Berechne die Längenänderung einer Zinkschare, die eine Einbaulänge von 10,00 m hat und einer Temperaturänderung von -20° C auf +80° C.
ΔT = 100 K
Δl = α x l₀ x ΔT
Δl = 0,022 x 10,00 x 100
Δl = 22 mm