Anwendung der Tangens-Funktion
Einführung
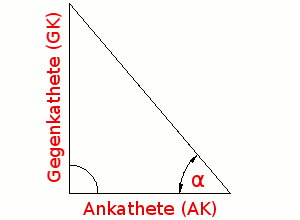
Berechnungen im rechtwinkligen Dreieck können mit Hilfe der Gleichung
durchgeführt werden. Diese Gleichung beschreibt das Verhältnis zwischen Gegen- und Ankathete in Abhängigkeit vom Winkel α. Die Verhältniszahl tan α kann entweder mit Hilfe des Taschenrechners ermittelt oder Tabellen entnommen werden.
Bei Problemen mit der Bestimmung der Verhältniszahl mit dem Taschenrechner, überprüfen Sie die Einstellungen des Gerätes. Hilfen dazu finden Sie hier
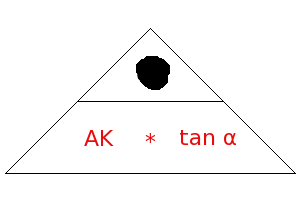
Bei der Anwendung der Gleichung ist das nebenstehend abgebildete Hilfsdreieck hilfreich. Man kann dem Dreieck die anzuwendene Gleichung entnehmen, wenn man die gesuchte Größe abdeckt.
Fallbeispiele
Fall 1 - ges.: GK
ges: GK
Lsg.: Deckt man in dem Dreieck GK ab, so steht unterhalb der Trennungslinie noch AK * tan α
Also:
GK = AK * tan α
Beispiel
Die Verhältniszahl tan 52° ist 1.28
Also berechnete sich die Gegenkathete wie folgt
GK = 1.28 * 5.68 = 7.27
Fall 2 - ges.: AK
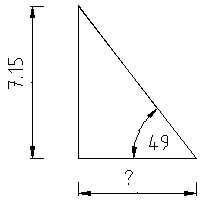
ges: AK
Lsg.: Deckt man in dem Dreieck AK ab, so steht dort noch GK / tan α
Also:
Beispiel
Die Verhältniszahl tan 49° ist 1.15
also berechnet sich die Ankathete wie folgt:
AK = 7.15 / 1.15 = 6.22
Fall 3 - ges.: Winkel
ges: α
Lsg.: Deckt man in dem Dreieck tan α ab, so steht dort noch GK/AK
Also:
Den Winkel kann man entweder der Tabelle entnehmen oder mit verschiedenen Funktionen auf dem Taschenrechner ermitteln. Die ist je nach Taschenrechner unterschiedlich.
Beispiel
Zunächst berechnet man GK/AK und das ist in diesem Fall
6.78/4.78 = 1.42
Schaut man jetzt in eine Tabelle oder benutzt den Taschenrechner, so findet man heraus, dass zu dieser Verhältniszahl der Winkel 55° gehört.