Dichte: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
[[Category:Werkstoffkunde]] | [[Category:Werkstoffkunde]] | ||
| − | Die Gleichung | + | ===Die Gleichung=== |
m = ρ * V | m = ρ * V | ||
| Zeile 6: | Zeile 6: | ||
beschreibt den Zusammenhang zwischen der Masse eines Körpers und seinem Volumen. Die Dichte ρ ist dabei eine Materialkonstante. | beschreibt den Zusammenhang zwischen der Masse eines Körpers und seinem Volumen. Die Dichte ρ ist dabei eine Materialkonstante. | ||
| + | ===Das Hilfsdreieck=== | ||
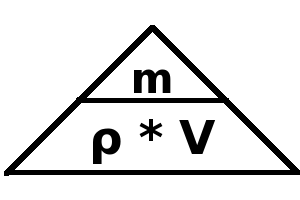
Um das Volumen eines Körpers oder die Dichte eines Materials auszurechnen, wenn die beiden anderen Größen gegeben sind, muss die Gleichung umgestellt werden. Dazu kann man das folgende Dreick zu Hilfe nehmen. | Um das Volumen eines Körpers oder die Dichte eines Materials auszurechnen, wenn die beiden anderen Größen gegeben sind, muss die Gleichung umgestellt werden. Dazu kann man das folgende Dreick zu Hilfe nehmen. | ||
| Zeile 12: | Zeile 13: | ||
Die Anwendung dieses Dreiecks ist simpel. Man verdeckt den Buchstaben für die gesuchte Größe und kann die erforderliche Gleichung ablesen. Im Folgenden ist sie für die Bestimmung des Volumens aufgezeigt. | Die Anwendung dieses Dreiecks ist simpel. Man verdeckt den Buchstaben für die gesuchte Größe und kann die erforderliche Gleichung ablesen. Im Folgenden ist sie für die Bestimmung des Volumens aufgezeigt. | ||
| − | + | ===Anwendungsbeispiel=== | |
| − | |||
{| | {| | ||
|[[Bild:Dreieck_dichte1.png]] | |[[Bild:Dreieck_dichte1.png]] | ||
| Zeile 20: | Zeile 20: | ||
''V = m / ρ'' | ''V = m / ρ'' | ||
|} | |} | ||
| + | |||
| + | ===Hinweis zu den Maßeinheiten=== | ||
| + | Die Dichte kann in t/m³, kg/l, oder g/cm³ angegeben werden. Die Maßzahl ist in allen drei Fällen die gleiche. Die Dichte von Beton ist dann z.B. 2.1 t je m³ oder 2,1 kg je Liter bzw. 2.1 g je cm³. Folgende Zusammenhänge bestehen also zwischen den Einheiten für die Masse und das Volumen:<br /><br /> | ||
| + | <table border="1" style="text-align: left; margin-left: auto; margin-right: auto;"> | ||
| + | <tr> | ||
| + | <td width="50%" valign="top" style="font-weight: bold;">Volumen<br /> | ||
| + | </td> | ||
| + | <td width="50%" valign="top" style="font-weight: bold;">Masse<br /> | ||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="50%" valign="top" style="text-align: center;">m³<br /> | ||
| + | </td> | ||
| + | <td width="50%" valign="top" style="text-align: center;">t<br /> | ||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="50%" valign="top" style="text-align: center;">l<br /> | ||
| + | </td> | ||
| + | <td width="50%" valign="top" style="text-align: center;">kg<br /> | ||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="50%" valign="top" style="text-align: center;">cm³<br /> | ||
| + | </td> | ||
| + | <td width="50%" valign="top" style="text-align: center;">g<br /> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <div style="text-align: center;"><br /> | ||
| + | <div style="text-align: left;">Ist also das Volumen in m³ gegeben, kann man mit Hilfe der Dichtegleichung die Masse in der Einheit t ausrechnen, ist dagegen die Masse in der Einheit g angegeben, wird das Volumen durch die Gleichung in cm³ errechnet.<br /></div></div> | ||
Version vom 9. Dezember 2009, 12:14 Uhr
Die Gleichung
m = ρ * V
beschreibt den Zusammenhang zwischen der Masse eines Körpers und seinem Volumen. Die Dichte ρ ist dabei eine Materialkonstante.
Das Hilfsdreieck
Um das Volumen eines Körpers oder die Dichte eines Materials auszurechnen, wenn die beiden anderen Größen gegeben sind, muss die Gleichung umgestellt werden. Dazu kann man das folgende Dreick zu Hilfe nehmen.
Die Anwendung dieses Dreiecks ist simpel. Man verdeckt den Buchstaben für die gesuchte Größe und kann die erforderliche Gleichung ablesen. Im Folgenden ist sie für die Bestimmung des Volumens aufgezeigt.
Anwendungsbeispiel
|
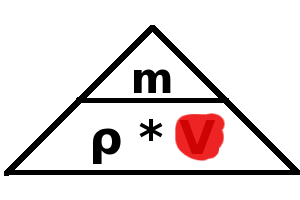
Berechnet werden soll das Volumen V, wenn Dichte ρ und Masse m des Körpers gegeben sind. Durch Abdecken des Buchstabens V erhält man die Gleichung
V = m / ρ |
Hinweis zu den Maßeinheiten
Die Dichte kann in t/m³, kg/l, oder g/cm³ angegeben werden. Die Maßzahl ist in allen drei Fällen die gleiche. Die Dichte von Beton ist dann z.B. 2.1 t je m³ oder 2,1 kg je Liter bzw. 2.1 g je cm³. Folgende Zusammenhänge bestehen also zwischen den Einheiten für die Masse und das Volumen:
| Volumen |
Masse |
| m³ |
t |
| l |
kg |
| cm³ |
g |