Winkelfunktionen: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
(→Sinus) |
|||
| Zeile 24: | Zeile 24: | ||
{| | {| | ||
| − | |[[Bild: | + | |[[Bild:Sinus_dreieck_anw.gif]] |
|Der Tangens beschreibt das Verhältnis von Gegen- zur Hypotenuse, in Abhängigkeit vom Winkel α. Dafür steht die Gleichung | |Der Tangens beschreibt das Verhältnis von Gegen- zur Hypotenuse, in Abhängigkeit vom Winkel α. Dafür steht die Gleichung | ||
| Zeile 31: | Zeile 31: | ||
Hilfreich bei der Anwendung der obenstehenden Gleichung ist das nebenstehende Hilfsdreieck. Seine Anwendung wird [[Anwendung der Sinus-Funktion|hier]] erläutert. | Hilfreich bei der Anwendung der obenstehenden Gleichung ist das nebenstehende Hilfsdreieck. Seine Anwendung wird [[Anwendung der Sinus-Funktion|hier]] erläutert. | ||
|} | |} | ||
| + | |||
==Cosinus== | ==Cosinus== | ||
Version vom 29. Oktober 2008, 12:10 Uhr
Einführung
|
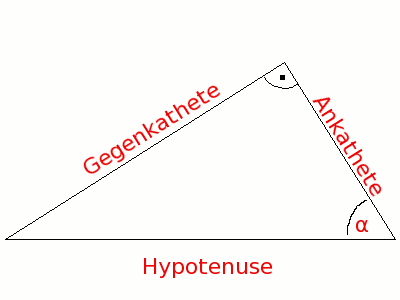
Die Winkelfunktionen Sinus, Cosinus und Tangens beschreiben die Verhältnisse jeweils zwischen zwei Seiten, wenn ein Winkel gegeben ist, neben dem rechten Winkel. |
Tangens
|
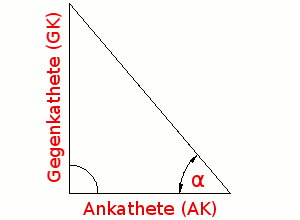
Der Tangens beschreibt das Verhältnis von Gegen- zu Ankathete, in Abhängigkeit vom Winkel α. Dafür steht die Gleichung
tan α = Gegenkathete(GK) / Ankathete(AK) Hilfreich bei der Anwendung der obenstehenden Gleichung ist das nebenstehende Hilfsdreieck. Seine Anwendung wird hier erläutert. |
Sinus
|
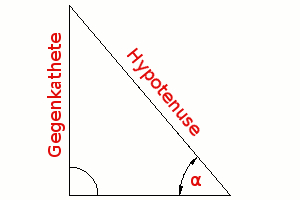
Der Tangens beschreibt das Verhältnis von Gegen- zur Hypotenuse, in Abhängigkeit vom Winkel α. Dafür steht die Gleichung
sin α = Gegenkathete(GK) / Hypotenuse(H) Hilfreich bei der Anwendung der obenstehenden Gleichung ist das nebenstehende Hilfsdreieck. Seine Anwendung wird hier erläutert. |
Cosinus
|
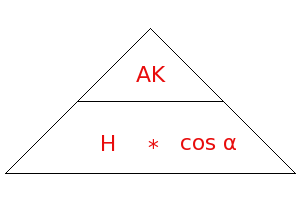
Der Cosinus beschreibt das Verhältnis von Ankathete zur Hypotenuse, in Abhängigkeit vom Winkel α. Dafür steht die Gleichung
cos α = Ankathete(AK) / Hypotenuse(H) Hilfreich bei der Anwendung der obenstehenden Gleichung ist das nebenstehende Hilfsdreieck. Seine Anwendung wird hier erläutert. |