Berechnung der Kehllänge: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
(Die Seite wurde neu angelegt: ==Herleitung== leftIn dieser Skizze ist ein Weg aufgezeigt, um die Länge der Kehle bei gleicher Dachneigung beider Gebäudeteile zu berech...) |
|||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[Category: Werkstoffkunde]] | ||
==Herleitung== | ==Herleitung== | ||
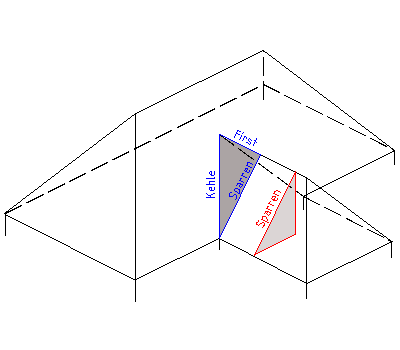
| − | [[Bild:Kehlberechnung.png|left]]In dieser Skizze ist ein Weg aufgezeigt, um die Länge der Kehle bei gleicher Dachneigung beider Gebäudeteile zu berechnen. Vorraussetzung ist, dass die Länge des Sparrens des niedrigeren Gebäudeteils bekannt ist. Nehmen wir also an, die Sparrenlänge wäre in dem rot eingezeichneten rechtwinkligen Dreieck mit Hilfe der Winkelfunktionen und/oder Pythagoras ermittetl worden, dann läßt sich die Kehllänge mit Hilfe der in dem blauen Dreieck angezeichneten Maße und dem Lehrsatz des Pyathagoras ausrechnen. | + | [[Bild:Kehlberechnung.png|left]] |
| + | <br style="clear:both;"> | ||
| + | In dieser Skizze ist ein Weg aufgezeigt, um die Länge der Kehle bei gleicher Dachneigung beider Gebäudeteile zu berechnen. Vorraussetzung ist, dass die Länge des Sparrens des niedrigeren Gebäudeteils bekannt ist. Nehmen wir also an, die Sparrenlänge wäre in dem rot eingezeichneten rechtwinkligen Dreieck mit Hilfe der [[Winkelfunktionen]] und/oder [[Pythagoras]] ermittetl worden, dann läßt sich die Kehllänge mit Hilfe der in dem blauen Dreieck angezeichneten Maße und dem Lehrsatz des Pyathagoras ausrechnen. | ||
Bei gleicher Dachneigung gilt: | Bei gleicher Dachneigung gilt: | ||
| Zeile 9: | Zeile 12: | ||
Die Kehllänge wäre dann: | Die Kehllänge wäre dann: | ||
| − | + | [[Bild:Kehle gleich wurzel.gif]] | |
<br style="clear:both"/> | <br style="clear:both"/> | ||
| + | |||
==Beispiel== | ==Beispiel== | ||
Dachneigung: 47°<br> | Dachneigung: 47°<br> | ||
| Zeile 22: | Zeile 26: | ||
===Kehllänge=== | ===Kehllänge=== | ||
Kehle = SQR (2.80² + 4.1²) = 4.96m | Kehle = SQR (2.80² + 4.1²) = 4.96m | ||
| + | |||
| + | ==weiterführende Links== | ||
| + | * [[Berechnung der Gratlänge]] | ||
| + | * [[Bestimmung der Kehlneigung]] | ||
Aktuelle Version vom 11. September 2017, 21:03 Uhr
Herleitung
In dieser Skizze ist ein Weg aufgezeigt, um die Länge der Kehle bei gleicher Dachneigung beider Gebäudeteile zu berechnen. Vorraussetzung ist, dass die Länge des Sparrens des niedrigeren Gebäudeteils bekannt ist. Nehmen wir also an, die Sparrenlänge wäre in dem rot eingezeichneten rechtwinkligen Dreieck mit Hilfe der Winkelfunktionen und/oder Pythagoras ermittetl worden, dann läßt sich die Kehllänge mit Hilfe der in dem blauen Dreieck angezeichneten Maße und dem Lehrsatz des Pyathagoras ausrechnen.
Bei gleicher Dachneigung gilt:
Firstabschnitt = halbe Gebäudebreite
Die Kehllänge wäre dann:
Beispiel
Dachneigung: 47°
Breite: 5.60 m
Sparrenlänge
AK = 5.60 m / 2 = 2.80 m
GK = 2.80 m * tan 47° = 3.00 m Sparren = SQR (2.80² + 3²) = 4.10 m
Kehllänge
Kehle = SQR (2.80² + 4.1²) = 4.96m