Giebelfläche eines Mansardgiebeldaches: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[Category: Werkstoffkunde]] | ||
| + | ==Aufgabe== | ||
[[Bild:Mansard gemwkftktn01.png]] | [[Bild:Mansard gemwkftktn01.png]] | ||
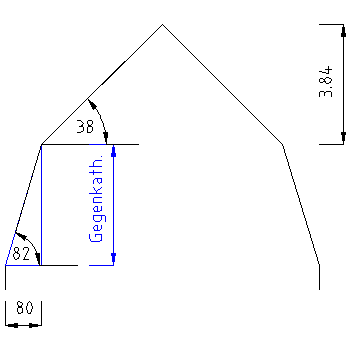
Gegeben Sie die Giebelfäche eines Mansardgiebeldaches wie in der obigen Zeichnung vorgegeben. | Gegeben Sie die Giebelfäche eines Mansardgiebeldaches wie in der obigen Zeichnung vorgegeben. | ||
| − | + | ==Vorüberlegungen== | |
[[Bild:Mansard gemwkftktn02.png]] | [[Bild:Mansard gemwkftktn02.png]] | ||
| Zeile 14: | Zeile 16: | ||
und in dem blauen Dreicke fehlt die Gegenkathete. | und in dem blauen Dreicke fehlt die Gegenkathete. | ||
| + | ==Lösung== | ||
| + | ===Winkelfunktion=== | ||
| + | ====rotes Dreieck==== | ||
| + | ges.: AK | ||
| + | |||
| + | AK = 3.84m / tan38 = 4.91 m | ||
| + | |||
| + | ====blaues Dreieck==== | ||
| + | |||
| + | ges.: GK | ||
| + | |||
| + | GK = 0.80m * tan 80 = 5.69 m | ||
| + | |||
| + | ===Flächen=== | ||
| + | ====oben (Dreieck)==== | ||
| + | |||
| + | g = 2 * 4.91 m = 9.82 m | ||
| + | |||
| + | A = (3.84 m * 9.82 m)/2 = 18.85m² | ||
| + | ====unten (Trapez)==== | ||
| + | |||
| + | l<sub>1</sub> = 9.82 m | ||
| + | |||
| + | l<sub>2</sub> = 9.82 m + 2*0.8m = 11.42 m | ||
| + | |||
| + | A = (11.42 m + 9.82 m)*5.69m/2 = 60.43 m² | ||
| + | ====gesamt==== | ||
| + | |||
| + | 18.85 m² + 60.43 m² = 79.28 m² | ||
| + | |||
| + | ==weiterführende Links== | ||
| + | * [[Formelsammlung]] | ||
| + | * [[Anwendung der Tangens-Funktion]] | ||
Aktuelle Version vom 10. Januar 2010, 13:59 Uhr
Aufgabe
Gegeben Sie die Giebelfäche eines Mansardgiebeldaches wie in der obigen Zeichnung vorgegeben.
Vorüberlegungen
Um die fehlenden Maße zu ermitteln, zeichnet man zwei rechtwinklige Dreiecke in Zeichnung.
In dem roten Dreieck fehlt die Ankathete.
und in dem blauen Dreicke fehlt die Gegenkathete.
Lösung
Winkelfunktion
rotes Dreieck
ges.: AK
AK = 3.84m / tan38 = 4.91 m
blaues Dreieck
ges.: GK
GK = 0.80m * tan 80 = 5.69 m
Flächen
oben (Dreieck)
g = 2 * 4.91 m = 9.82 m
A = (3.84 m * 9.82 m)/2 = 18.85m²
unten (Trapez)
l1 = 9.82 m
l2 = 9.82 m + 2*0.8m = 11.42 m
A = (11.42 m + 9.82 m)*5.69m/2 = 60.43 m²
gesamt
18.85 m² + 60.43 m² = 79.28 m²