DTP Frontanbauten: Unterschied zwischen den Versionen
Hennes (Diskussion | Beiträge) |
|||
| Zeile 6: | Zeile 6: | ||
[[Bild:SchmalerFa_00.png]] | [[Bild:SchmalerFa_00.png]] | ||
| − | Gegeben sei ein Teil der Draufsicht eines Haupthauses mit Ost/West verlaufender Traufe und ein rechtwinklig dazu verlaufenden schmaleren | + | Gegeben sei ein Teil der Draufsicht eines Haupthauses mit Ost/West verlaufender Traufe und ein Teil eines rechtwinklig dazu verlaufenden schmaleren Frontanbaus gleicher Dachneigung. |
[[Bild:SchmalerFa_01.png]] | [[Bild:SchmalerFa_01.png]] | ||
| − | Zunächst wollen wir die beiden Gebäudeteile | + | Zunächst wollen wir die beiden Gebäudeteile separat voneinander betrachten als ein breiteres und längeres und ein schmaleres Gebäude. |
[[Bild:SchmalerFa_02.png]] | [[Bild:SchmalerFa_02.png]] | ||
| − | Für beide kann man die Lösung zunächst unabhängig ermitteln. Hier für das schmalere | + | Für beide kann man die Lösung zunächst unabhängig ermitteln. Hier für das schmalere Gebäudeteil und ... |
[[Bild:SchmalerFa_03.png]] | [[Bild:SchmalerFa_03.png]] | ||
| − | ... hier für das breitere | + | ... hier für das breitere Gebäudeteil. |
[[Bild:SchmalerFa_04.png]] | [[Bild:SchmalerFa_04.png]] | ||
| Zeile 34: | Zeile 34: | ||
[[Bild:SchmalerFa_07.png]] | [[Bild:SchmalerFa_07.png]] | ||
| − | ... | + | ...folgende Lösung erhält. |
==weiterführende Links== | ==weiterführende Links== | ||
* [[wahre Fläche - schmaler Frontanbau|Ermittlung der wahren Fläche]] | * [[wahre Fläche - schmaler Frontanbau|Ermittlung der wahren Fläche]] | ||
* [[DTP breiter Frontanbau|breiter Frontanbau]] | * [[DTP breiter Frontanbau|breiter Frontanbau]] | ||
Version vom 1. Dezember 2008, 18:56 Uhr
Dreitafelprojektion - Frontanbau
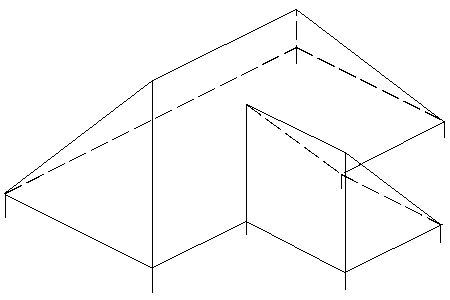
Gegeben sei ein Teil der Draufsicht eines Haupthauses mit Ost/West verlaufender Traufe und ein Teil eines rechtwinklig dazu verlaufenden schmaleren Frontanbaus gleicher Dachneigung.
Zunächst wollen wir die beiden Gebäudeteile separat voneinander betrachten als ein breiteres und längeres und ein schmaleres Gebäude.
Für beide kann man die Lösung zunächst unabhängig ermitteln. Hier für das schmalere Gebäudeteil und ...
... hier für das breitere Gebäudeteil.
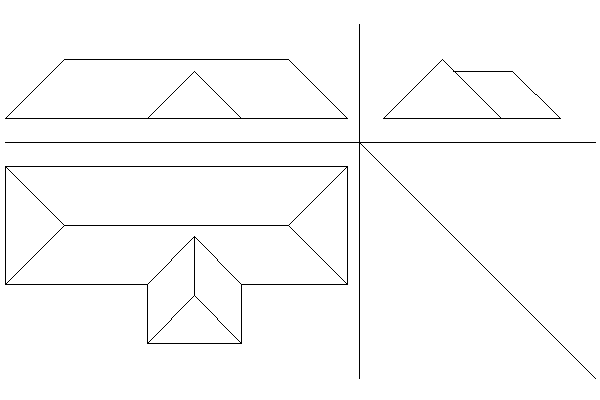
Setzt man dies wieder zusammen, ergibt sich die obige Lösung. Dabei 'verschwindet' jedoch ein Teil des grün gezeichneten Gebäudes im blau gezeichneten Gebäude. Diese Teile können also nicht existent sein.
Ebenso muss der First am Eindringungspunkt in das blaue Gebäudeteil enden. Auch muss die Traufe des blauen Gebäudes am grünen Anbau unterbrochen sein.
Kehlen verbinden die einspringenden Gebäudeecken mit dem First, so dass man ....
...folgende Lösung erhält.