Erläuterungen - Kegel
Zur Navigation springen
Zur Suche springen
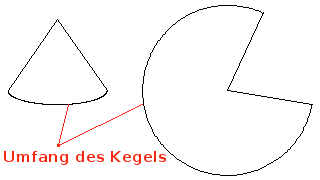
Die Mantelfäche eines Kegels berechnet sich mit der Gleichung
Betrachtet man dazu die aufgeschnittene Fläche des Kegels, so ist der Umfang des Teilkreises genauso lang die der Umfang des Kegels. Der Umfang des Kegels ist
UKegel = 2 πr.
Wäre der aufgeklappte Kreis (rechts) vollständig, so hätte er den Umfang
UKreis = 2 πs.
Die Fläche des vervollständigten Kreises wäre
AKreis=πs²
Die in der rechten Zeichnung dargestellte Teilfläche des Kreises ist der r/s-te Teil des vollständigen Kreises, da
UKegel/UKreis= (2 πr)/(2 πr) = r/s.
Deshalb gilt
AKegel = π s² * (r/s) = (r π s²)/s = r π s
nach dem Kürzen.